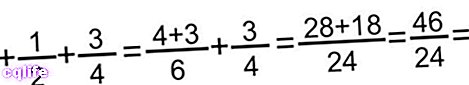Објашњавамо шта је сабирање или сабирање у математици, њену историју, својства и примере. Такође, методе сабирања разломака.

Колики је збир?
Сабирање или сабирање је фундаментална математичка операција, која се састоји од уграђивања нових елемената у а комплет нумерички, односно спајању два броја да би се добио нови, који изражава укупну вредност претходна два. Сабирање је основни принцип помоћу којег учимо да се повезујемо са бројевима, јер сама чињеница бројања једног по једног (1, 2, 3, 4 ...) укључује сабирање 1 (1 + 0, 1 + 1, 1 + 2, 1 + 3…).
Збир је операција аритметичког типа, која омогућава комбиновање бројева различитих типова: природним, цели бројеви, разломци, реални, рационални, ирационални и комплексни, као и структуре повезане са њима, као што су векторски простори или матрице. Ат алгебра Модернизам је представљен симболом +, уметнутим између елемената који се додају, и израженим вербално као „више“: „1 + 1 = 2“ се чита „један плус један је два“.
С друге стране, елементи који се додају познати су као „сабира“, а број добијен на крају назива се „резултат“.
Историја суме
Сабирање је једна од најстаријих и најосновнијих познатих математичких операција. Сматра се да је људско биће Од неолита је већ баратао елементарним математичким принципима, међу којима би обавезно били сабирање и одузимање, пошто је ове операције лако доказати у условима пољопривредних залиха које су се повећавале и смањивале у зависности од доба године.
Међутим, проучавање сабирања и његове примене и на природне и на разломке започело је од старих Египћана, а наставило да се развија на сложеније начине код Вавилонаца, а посебно код Кинеза и Индуса, који су први сабирали бројеве. . Али само у Ренесанса банкарски бум наметнуо је збир децимала и вулгарних логаритама.
Особине збира
Сабирање као математичка операција има скуп својстава, а то су:
- Комутативно својство. Он утврђује да редослед сабирака не мења резултат, односно да је а + б потпуно исти као б + а, и у оба случаја се добија исти резултат.
- Асоцијативно својство. Утврђује да је приликом додавања три или више елемената могуће груписати два од њих да би их прво решили, без обзира на то који су, без промене коначног резултата. То јест, ако желимо да додамо а + б + ц, можемо изабрати два начина: (а + б) + ц или а + (б + ц), а да уопште не утичемо на резултат.
- Својство идентитета. Он утврђује да је нула неутралан елемент у операцији, тако да ће додавање са било којим другим бројем увек резултирати истим последњим бројем: а + 0 = а.
- Затварање имовине. Он утврђује да ће резултат збира увек припадати истом нумеричком скупу сабирака, све док они заузврат деле исти скуп. То јест, ако сабирци а и б припадају Н (природни), З (цели бројеви), К (ирационални), Р (реални) или Ц (комплексни), резултат збира ће такође припадати истом скупу.
Примери сабирања
Ево неколико једноставних примера сабирања:
- Жена има четири цвета, али јој је рођендан и поклањају јој још осам. Колико цвећа има на крају дана? 4 цвета + 8 цветова = 12 цветова.
- Пастир има 15 оваца, а његов колега 13. Ако одлуче да споје своја стада, колико ће укупно оваца имати? 15 оваца + 13 оваца = 28 оваца.
- Дрво јабуке даје свом власнику 5 јабука месечно. Колико ће јабука имати на крају једне године? Пошто је година 12 месеци, морамо сабрати 5 дванаест пута, примењујући својство асоцијативности: (5 + 5) + (5 + 5) + (5 + 5) + (5 + 5) + (5 + 5) + ( 5 + 5) = (10 + 10) + (10 + 10) + (10 + 10) = 20 + 20 + 20 = 60 јабука у години.
Збир разломака
Приликом сабирања разломака постоје различити методе које можемо применити за добијање резултата у зависности од тога да ли је у питању прави, неправилан и мешовити разломци.
- Метода сабирања разломака са истим имениоцем. Ово је најједноставнији случај, у којем једноставно сабирамо бројиоце и задржавамо исти именилац. На пример:
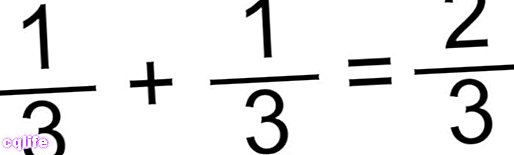
или
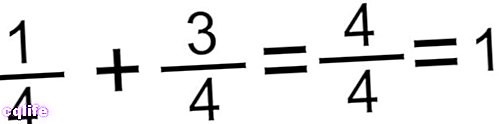
- Метода лептира. Овај метод нам омогућава да саберемо било коју врсту разломака са различитим имениоцима, једноставно помножимо бројилац првог са имениоцем другог и обрнуто, а затим саберемо производе (да бисмо добили бројилац), а затим множимо имениоце да бисмо добили именилац коначног разломка. Када се ове операције спроведу, често ћемо морати да смањимо резултат. На пример:
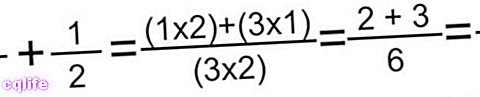
- Метода сабирања три фракције. У овом случају једноставно додајемо прва два и додајемо последњу резултату, примењујући претходни метод и смањујући или поједностављујући резултат ако је потребно. На пример: