- Шта је периметар?
- Практичне примене периметра
- Периметар круга
- Обим правоугаоника
- Периметар квадрата
- Периметар неправилног многоугла
Објашњавамо шта је периметар, како се он израчунава у различитим геометријским фигурама и његове примене у другим дисциплинама.

Шта је периметар?
У геометрији, периметар је збир од дужине са стране било које геометријска фигура раван. То је кључни концепт за матх, који је заједно са облашћу, која му је блиска, неопходно савладати да би се кренуло ка напреднијој математици као нпр. алгебра анд тхе тригонометрија, пошто дозвољавају изградњу полигона.
Реч периметар потиче од старогрчког (унија гласова пери, „све и метрон, „Мера”), пошто су га древни грчки филозофи први израчунали. Прва мисао овог типа приписује се филозофу Архимеду (око 287-212. пре Христа).
Концепт се односи и на растојање и дужину, или на контуру фигура; али се у случају кругова преименује обим. Половина периметра се назива полупериметар. Периметар је представљен словом П.
Практичне примене периметра

Прорачун периметра има много практичних примена, посебно за рад архитектура, инжењеринг и грађевинарство. На пример, може се користити за израчунавање ивица или граница а простор или објекат, као што је комад земље или зграда.
Ако желимо, на пример, да поставимо ограду око наше баште, биће потребно да израчунамо обим њене површине, да знамо колико материјала да купимо и како да их поставимо.
Периметар круга
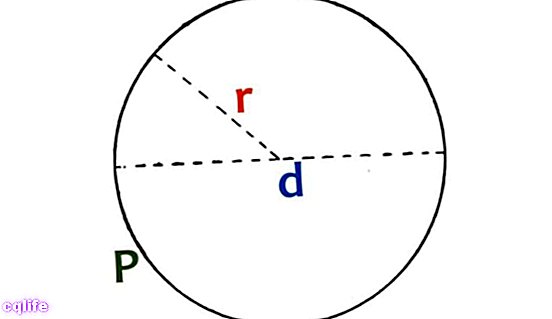
Обим круга се назива обим, а израчунава се применом следеће формуле:
П = 2π. р = дπ
Где је π математичка константа еквивалентна 3,14159…, р је дужина полупречника круга, а д је дужина пречника круга. У случају полукруга, формула ће се променити у:
П = 2р + р. π = р (2 + π)
Обим правоугаоника
Обим правоугаоника је лако израчунати.У случају правоугаоника, не морате да израчунате обим више од сабирања дужина његове две дугачке и две кратке странице. То јест, ако правоугаоник има две странице а (а1, а2) и две странице б (б1, б2), обим ће се израчунати додавањем а1 + а2 + б1 + б2.
Периметар квадрата
Странице квадрата су једнаке једна другој, као и странице правоуглог троугла.Случај квадрата је идентичан случају правоугаоника. У ствари, у случају правилних многоуглова, чије странице мере потпуно исте (као што су једнакостранични троуглови), биће довољно да се дужина једне странице помножи са бројем страна на слици:
- Квадрат. 4 идентичне странице мере а, дакле П = а к 4.
- троугао једнакостраничан. 3 идентичне странице које мере б, па је П = б к 3.
Исто важи и за друге сличне фигуре, без обзира на њихов број страна. С друге стране, за једнакокраке и скалиране троуглове, свака дужина сваке стране мора бити додата.
Периметар неправилног многоугла
Да бисте израчунали обим неправилног многоугла, морате знати дужину његових страница.Код неправилних многоуглова, односно оних који немају странице и углови идентично, биће довољно додати мере свих страница многоугла, без обзира на њихов облик. У случају да немамо мере за неке од ових страна, задатак ће бити компликован јер их прво морамо израчунати, али онда можемо да наставимо са њиховим сабирањем без икаквих потешкоћа.
